CASTLE.PRI.EE

Записи с меткой «счёт»

К статье «Загадки истории — римские цифры» в комментариях были высказаны сомнения по отдельным положениям. Попробую пояснить с помощью изложения статьи «Арифметика Санта Яги» блогера под ником galina6111.

Главным минусом римских цифр обычно называют отсутствие позиционной записи, которая, будто бы, затрудняет вычисления на бумаге.

Создатель первой русской книги по математике Магницкий называл римские цифры – «школьными». Посмотрим, как можно считать с их помощью.

Множество многомудрых и остепенённых авторов учебников по математике и истории математики, например, Прасолов, Выгодский, Депман и другие считают, что запись при помощи римских цифр не является позиционной.
Процесс счета и записи был напрочь разделён.

Посмотрим, что же такое римские цифры и какие они бывают? Римские цифры – это знаки, которые использовали в разных операциях древнеримской арифметики.

Всего древнеримских цифр – 7:
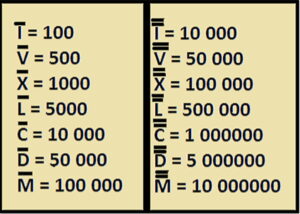
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000

Кроме этого, горизонтальная черта над цифрой увеличивало цифру в 100 раз.

Две черты – в 10 000 раз и так далее.

В системе счисления Древнего Рима присутствуют разряды: единиц, пятёрок, десятков, пятидесятков, сотен, пятисотен, тысяч и так далее, следовательно, она является – позиционной.

На рисунке представлена реконструкция (galina6111) древнеримской абаки на основе переработанной и исправленной реконструкции (Prof. Dr. Jörn Lütjens, Hamburg, Germany, May 2004). Помощь в создании рисунка оказал © Дмитрий Чесноков, 2020.

Конструкция наглядно демонстрирует ПОЗИЦИОННЫЙ принцип древнеримского счисления для целых чисел. Разряды возрастают справа от разряда ЕДИНИЦ, налево до разряда ДЕСЯТКИ МИЛЛИОНОВ.
Можно располагать прорези-разрядов и слева направо.

Принцип нагляден и прост:
Пять калькулей разряда Единиц равны одному калькулю разряда Пятёрок.
То есть, при достижении в разряде Единиц количества в пять калькулей – разряд Единиц обнуляется с одновременным увеличением разряда Пятёрок на один калькуль. Два калькуля разряда Пятёрок равны одному калькулю из разряда ДЕСЯТОК. То есть, при достижении в разряде Пятёрок количества в два калькуля – разряд Пятёрок обнуляется с одновременным увеличением разряда Десяток на один калькуль.

Пять калькулей разряда Десяток равны одному калькулю разряда Пятидесятков. Два калькуля разряда Пятидесятков равны одному калькулю из разряда СОТЕН. Пять калькулей разряда Сотен равны одному калькулю разряда Пятисотен. Два калькуля разряда Пятисотен равны одному калькулю из разряда ТЫСЯЧ. И так далее, наращивая количество разрядов по мере надобности.

Древним римлянам было известно понятие НУЛЯ. Ещё раз глянем на абаку. В прорезе-разряде может находится количество калькулей от НИЧЕГО до ЧЕТЫРЕ. НИЧЕГО – это перевод с латыни – НОЛЬ. Раз имеется слово, значит, существовало и понятие ему соответствующее, или предмет.

Римское число – это просто сумма разрядов. Между которыми отсутствуют знаки «плюс».

Проиллюстрируем примером сложение двух чисел.

Сложение двух чисел A + B = C – это нахождение третьего числа, равного сумме первых двух чисел.

Пример арабскими цифрами:
28 + 37 = 2 х 10 + 8 + 3 х 10 + 7 = (2 + 3) х 10 + (8 + 7) = 5 х 10 + 10 + 5 = 6 х 10 + 5 = 65
Пример древнеримскими цифрами:
XXVIII + XXXVII = X+X+V+I+I+I + X+X+X+V+I+I = X+X+X+X+X+ V+V+I+I+I+I+I = L+X+V = LXV

Сложение римскими цифрами похоже на сложение арабскими:
Складываются цифры соответствующих разрядов. При переполнении разряда, начинает увеличиваться старший разряд и так далее.
Отличие в одном – запись числа требует большего числа цифр. А человек – ленив.

Ещё один пример: 167 + 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000): CLXVII + XIIII = CLXXVVI = CLXXXI = 181
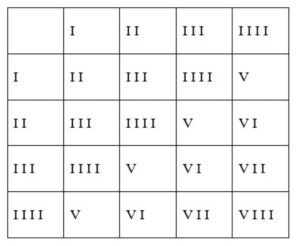
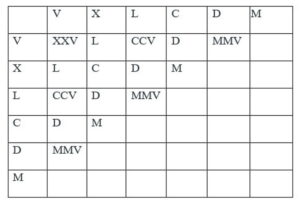
Принцип сложения – понятен, остаётся всего лишь составить таблицы сложения для упрощения процесса вычисления. Аналогично таблице умножения арабскими цифрами.

Сложение:

Сложение для старших разрядов:

Вычитание:

167 – 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000): CLXVII — XIIII = CL + X — X + VII — IIII = CLIII = 153

Вычитание римскими цифрами проще сложения. Знай себе вычитай из соответствующего разряда соответствующий разряд.

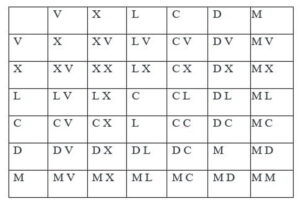
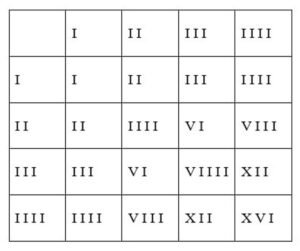
Таблица умножения:

Таблица умножения старших цифр:

Выпускники 11 класса, предложили преобразование типа:

a + b = b + a
ab = ba
a(b + c) = ab + ac

XXXX = X х (IIII)
В переводе на арабские цифры:
40 = 10 х 4
Пример вычисления:
167 х 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000):
CLXVII х XIIII = CLXVII х X + CLXVII х IIII = MMCCCXXXVIII
Подробности:
CLXVII х X = MDCLXX
CLXVII х IIII = CCCC + CC + XXXX + XX + VIII = DCLXVIII
MDCLXX + DCLXVIII = MMCCCXXXVIII = 2338

Сложности с вычислениями отсутствуют, только запись результата длинная, нужно привыкнуть к этому. Но сами вычисления легки и понятны.

Деление использует тот же алгоритм, что и деление уголком при помощи арабских цифр. И в то же время идентично делению многочлена на одночлен.

167 / 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000):
CLXVII / XIIII = (CLX + VII) / (X + IIII) = CLX / (X + IIII) + VII / (X + IIII)
CLX / (X + IIII) = XVI х X / XIIII = (XVI / XIIII) х X = X + XX/ XIII =
= XI + VI / XIIII
X I + VI / XIIII + VII / (X + IIII) = XI + XIII / XIIII = 11 целых и 13/ 14 в остатке.

Возведение в степень и извлечение корней.

Возведение в любую степень легко выполняется по правилам умножения.
И возведения в степень по правилам нахождения степени суммы слагаемых.
Удобно использовать заранее составленные таблицы степеней.
Например, 14 в квадрате: XIIII х XIIII = X х X + II х X х IIII + IIII х IIII =
= C + LXXX + XVI = CLXXXXVI = 196

Извлечение корней можно проводить по известным алгоритмам.

На основании вышеизложенного следует вывод:
Арифметические вычисления римскими цифрами возможны и легко осуществимы, при соответствующем навыке.

Вычисления римскими цифрами более просты, образны и наглядны чем вычисления арабскими цифрами. Опытным путём установлено, что обучаемые усваивают арифметические операции со скоростью на порядки быстрее, чем арабскими цифрами и с минимальными усилиями. Перспективно создание учебника арифметики на базе римских цифр для классов, начиная с первого. В проекте участвовали ученики 11 класса.