CASTLE.PRI.EE

Записи с меткой «Римские цифры»

На то, что реальная хронология цивилизации короче писаной, указывают многие обстоятельства, которые нужно учитывать. В 70-е годы объем информации удваивался каждые 5-7 лет. В 80-е гг. удвоение происходило уже за 20 месяцев, а в 90-е — ежегодно. Пролонгируя эти данные в прошлое, видишь экспоненциальное сокращение. Согласно этому античная культура существовала лет 300 назад.

Кибернетик и философ Р.Ф. Абдеев в 1994 году в своей работе «Философия информационной цивилизации» писал: «динамика роста объёма информации… ныне удваивается каждые 20 месяцев против 50 лет во времена Маркса». Если, говоря о временах Маркса, Абдеев имел ввиду примерно 1843 год, когда Маркс стал известен, то выстраивается динамика, в которой в 1782 году ежегодный прирост информации составлял 1 %, – как на крестьянском дворе в самой глухомани.

Имеются и другие оценки, например, А.Т. Фоменко применил модель угасающего сигнала к сохранности сведений о прошлом. Однако, в любом случае, прошлое ближе к нам в разы.

Архивы горят, свидетели умирают, меняются люди. Английский этнограф Джеймс Джордж Фрэзер (1854-1941) сократил число томов своего исследования «Золотая ветвь» с 12 до одного. При этом, он всё равно описал многие сотни обрядов, ещё действовавших в 19 веке. А сейчас они прочно забыты. Эта реальность – исчезла.

Кто из 15-летних знает, как считать на счётах? Как защитить ребёнка от сглаза? Заговорить бородавку или тем же способом отвести беду? Это уже исчезло даже из художественной литературы. Чем глубже в прошлое, тем ниже темпы создания информации и выше – её исчезновения. Оба процесса экспоненциальные. Что могло к нам дойти через 2 тысячи лет?

Технологии античности по своей сложности вплотную примыкают к самому концу 18 века – без промежуточных уровней развития. Техническая проверка открытий Глаубера, Ньютона, Галилея, Джабира и других, показывает, что отсутствует возможность их создания в то время. Например, У. Гершель создал телескоп с увеличением, позволявшим фиксировать наблюдаемое изображение, только с помощью автоматической фотокамеры. Она была создана на 50 лет позже.

И так – во всех сферах. Барди и Перуцци в 1345 году используют финансовые инструменты, изобретённые спустя 500 лет. Работорговцы ввозят черных работников в США за 200 лет до первых посадок хлопка и сахарного тростника. Ну, а фондовые биржи торгуют фондами за 380 лет до того, как в Европе создали правовые нормы, позволяющие торговать ими.

Одна из версий удлинения история с помощью отбросов массивов данных в прошлое. Да, анахронизмов многие тысячи, да передвижки данных в прошлое хорошо видны, однако история в целом чересчур хорошо согласована. Добиться такого согласования управленческими методами сложно даже сейчас.

Другой способ – изменить словарные дефиниции, например, чтобы слово десять трактовалось всеми как сто. В этой ситуации даты изменятся, а сроки удлинятся – сами, повсеместно и без вмешательства переписчиков. В качестве побочного эффекта в прошлом появятся многомиллионные армии и города с реальным размером со стадион и летописным населением в десятки тысяч, что мы и видим.

Имеется гипотеза, что произошла утрата потомками преемственности знаний в результате перехода римского счета с восьмеричного на десятичный. Достаточно описать в словарях десятичную римскую систему счета, без описания предыдущей восьмеричной, и процесс запущен. Все ошибки в датировании (их целый каскад) – лишь производное.

Агрикола в своих книгах о металлургии (1530-1557) использует систему долей, кратных восьми: 8; 16; 32; 64; 128. Античные солнечные часы разбиты на 8 секторов. В Древнем Риме год делился на нундины – циклы по 8 дней. В
Древней Греции и в Древнем Риме одна ладонь была равна четырём пальцам. Локоть был равен либо 20, либо 28 пальцам, то есть, в основе 4, вместо 5-ти. Дюжины – это 12 фаланг 4 пальцев. Отсюда легко прийти к восьмеричной системе счета и отсутствует возможность – к десятичной. Шахматы: 8 клеток по каждой стороне, 16 белых фигур (дважды по 8), 16 черных.

Посмотрим на особенность словообразования существительных русского языка при их подсчёте:
1 — именительный падеж, ед. число — один стол
2 — родительный падеж, ед. число — два стола
3 — родительный падеж, ед. число — три стола
4 — родительный падеж, ед. число — четыре стола
5 — родительный падеж, мн. число — пять столов
6 — родительный падеж, мн. число — шесть столов
…
20 — родительный падеж, мн. число — двадцать столов
Счёт до четырёх формируется из словоформ единственного числа, множественное число появляется только начиная с пяти единиц учитываемых предметов. И так – для всех существительных. Например, один год, два года, три года, четыре года, пять ЛЕТ.

Самые ранние известные римские пасхальные таблицы, составленные в 222 г. Ипполитом Римским, основаны на 8-летнем цикле. Румбов на компасе восемь. Римских месяцев без встроенного в название номера – 8; пронумерованы лишь 4 последних. Монетные системы европейских стран до середины 19 века основаны на числе 8 и, как следствие, — 16 и 24. Для медных монет Российской империи чеканки 1810—1830 годов монетная стопа составляла 24 рубля из одного пуда.

Вплоть до революции в России масса крестьян считала осьмериками. В. И. Даль: «восьмериковый, относящийся до счёта осьмериком». Президент США Томас Джефферсон использует в письмах доли, кратные восьми. Барингс-банк, проводивший сделку по продаже Луизианы, взял в качестве вознаграждения 12,5 % или восьмую часть.

Газета Протестант пишет: «В денежном эквиваленте десятина равнялась 12% (Лев. 27:31)». Число явно расчётное и с достаточной точностью равно восьмой части. Вспомним, как выглядят счёты. Там две чёрных костяшки, и восемь белых. То есть, любые счёты применимы как для сложения в десятичной, так и в восьмеричной системе счисления.

Основное требование при переходе на десятичный счёт – прагматичность. Все должно стать намного лучше, но без особых изменений. И вот чтобы вернуться к восьмеричной системе так же без особых потерь, проще всего пожертвовать цифрами с префиксным вычитанием.

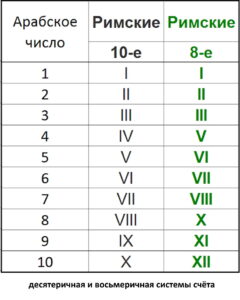
I — один
II — два
III — три
IV – три (второй вариант написания)
V — ЧЕТЫРЕ
VI — пять
VII — шесть
VIII — семь
IX — семь (второй вариант написания)
X — ВОСЕМЬ
XI — девять
XII — десять
XIII — одиннадцать
XIV — одиннадцать (второй вариант написания)
XV — ДВЕНАДЦАТЬ

Префиксное вычитание прежде выглядело иначе. Число IIII xx в ряде старых книг означает 80. То есть, буквы «i» в начале означали количество последующих чисел, в данном случае, — четыре двадцатки (80), а в реконструированном виде – четыре по шестнадцать (64). Умножаемое (xx) пишется маленькими буквами.

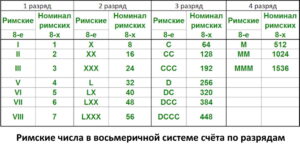
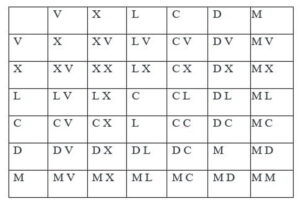
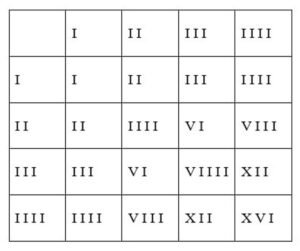
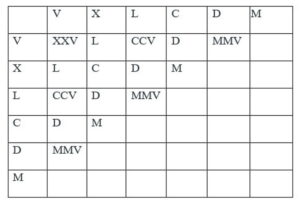
Это предположение подтверждается, сопоставлением римской записи в одном издании с арабской записью в другом. Вероятно, что счёт римскими цифрами изначально был восьмеричным. Это подтверждается таблицами: «Десятеричная и восьмеричная системы счёта», «Римские числа в восьмеричной системе счета по разрядам», «Соответствие римских чисел в 8-ой и 10-ой системах современным арабским (в разрядах)».

Представьте, что римский счёт восьмеричный, и вам надо превратить его в десятичный, то есть, добавить одно число на каждые пять чисел. Можно добавить четвертую «I». Вероятно, так и было, в документах имеется много таких чисел.

Потом, когда начали формировать даты от Р. Х., сообразили, что придётся добавлять четвертую X и четвертую С. И появится вот такой монстр: MDCCCCLXXXXVIIII (1999) из 16 знаков. Пришлось менять значение знаков. Это привело к тому, что вся хронология «поехала» во всех источниках.

Загадка, откуда именно и зачем заимствована десятичная система счета. Пишут, что «от арабов». Нужно вспомнить масштабный вброс малийского золота в Европу около 1324 года (дата традиционная). На тот момент это золото составляло 70 % всего находящегося в обороте. В Мали правили арабы и они могли, в такой ситуации, диктовать свои правила.

Одной из причин удлинения хронологии в 15,5-19,2 раза был переход на десятичный римский счёт. Даты сразу же стали читаться иначе. Возможно, на тот момент это посчитали мелочью. Ведь связи между идентично датированными документами остались. Затем оказалось, что исправить это очень сложно. Взять на себя смелость, что-то изменить в старом важном документе, касающемся, например, межевания земель или династических прав, было опасно для жизни.

Попытка, хотя бы частично, нормализовать даты, сразу же приводила к нарушению исторических связей. Возможно, нужно отказаться от мысли, что искажение хронологии результат заговора. Скорее всего это связано с техническими проблемами организации пересчёта. Ну, а когда выросло первое поколение, закончившее университеты по «новой программе», решение проблемы – исчезло: люди видели то, чему их научили.

Вероятно, какое-то время обе системы счета и датирования имели синхронное хождение. Возможно, с этим связано, что часть событий 18-19 веков имеет античных близнецов. Эти события оказались в прошлом, так как отсутствуют способы проконтролировать употребление чисел и дат.

Краткое изложение статьи Андрея Степаненко «Римский счёт – ключ к тайне хронологии».

P.S. Возможно, искажение хронологии результат заговора. Есть версия, что все термины: графы, князья, бароны и тому подобное, придуманы в конце 18, начале 19 века для оправдания захвата власти. Им требовались доказательства их древности. Для этого запутали датирование событий, написали множество «древних» документов.

К статье «Загадки истории — римские цифры» в комментариях были высказаны сомнения по отдельным положениям. Попробую пояснить с помощью изложения статьи «Арифметика Санта Яги» блогера под ником galina6111.

Главным минусом римских цифр обычно называют отсутствие позиционной записи, которая, будто бы, затрудняет вычисления на бумаге.

Создатель первой русской книги по математике Магницкий называл римские цифры – «школьными». Посмотрим, как можно считать с их помощью.

Множество многомудрых и остепенённых авторов учебников по математике и истории математики, например, Прасолов, Выгодский, Депман и другие считают, что запись при помощи римских цифр не является позиционной.
Процесс счета и записи был напрочь разделён.

Посмотрим, что же такое римские цифры и какие они бывают? Римские цифры – это знаки, которые использовали в разных операциях древнеримской арифметики.

Всего древнеримских цифр – 7:
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000

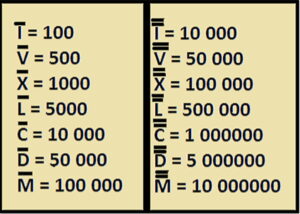
Кроме этого, горизонтальная черта над цифрой увеличивало цифру в 100 раз.

Две черты – в 10 000 раз и так далее.

В системе счисления Древнего Рима присутствуют разряды: единиц, пятёрок, десятков, пятидесятков, сотен, пятисотен, тысяч и так далее, следовательно, она является – позиционной.

На рисунке представлена реконструкция (galina6111) древнеримской абаки на основе переработанной и исправленной реконструкции (Prof. Dr. Jörn Lütjens, Hamburg, Germany, May 2004). Помощь в создании рисунка оказал © Дмитрий Чесноков, 2020.

Конструкция наглядно демонстрирует ПОЗИЦИОННЫЙ принцип древнеримского счисления для целых чисел. Разряды возрастают справа от разряда ЕДИНИЦ, налево до разряда ДЕСЯТКИ МИЛЛИОНОВ.
Можно располагать прорези-разрядов и слева направо.

Принцип нагляден и прост:
Пять калькулей разряда Единиц равны одному калькулю разряда Пятёрок.
То есть, при достижении в разряде Единиц количества в пять калькулей – разряд Единиц обнуляется с одновременным увеличением разряда Пятёрок на один калькуль. Два калькуля разряда Пятёрок равны одному калькулю из разряда ДЕСЯТОК. То есть, при достижении в разряде Пятёрок количества в два калькуля – разряд Пятёрок обнуляется с одновременным увеличением разряда Десяток на один калькуль.

Пять калькулей разряда Десяток равны одному калькулю разряда Пятидесятков. Два калькуля разряда Пятидесятков равны одному калькулю из разряда СОТЕН. Пять калькулей разряда Сотен равны одному калькулю разряда Пятисотен. Два калькуля разряда Пятисотен равны одному калькулю из разряда ТЫСЯЧ. И так далее, наращивая количество разрядов по мере надобности.

Древним римлянам было известно понятие НУЛЯ. Ещё раз глянем на абаку. В прорезе-разряде может находится количество калькулей от НИЧЕГО до ЧЕТЫРЕ. НИЧЕГО – это перевод с латыни – НОЛЬ. Раз имеется слово, значит, существовало и понятие ему соответствующее, или предмет.

Римское число – это просто сумма разрядов. Между которыми отсутствуют знаки «плюс».

Проиллюстрируем примером сложение двух чисел.

Сложение двух чисел A + B = C – это нахождение третьего числа, равного сумме первых двух чисел.

Пример арабскими цифрами:
28 + 37 = 2 х 10 + 8 + 3 х 10 + 7 = (2 + 3) х 10 + (8 + 7) = 5 х 10 + 10 + 5 = 6 х 10 + 5 = 65
Пример древнеримскими цифрами:
XXVIII + XXXVII = X+X+V+I+I+I + X+X+X+V+I+I = X+X+X+X+X+ V+V+I+I+I+I+I = L+X+V = LXV

Сложение римскими цифрами похоже на сложение арабскими:
Складываются цифры соответствующих разрядов. При переполнении разряда, начинает увеличиваться старший разряд и так далее.
Отличие в одном – запись числа требует большего числа цифр. А человек – ленив.

Ещё один пример: 167 + 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000): CLXVII + XIIII = CLXXVVI = CLXXXI = 181
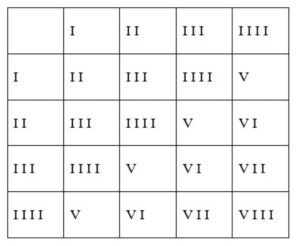
Принцип сложения – понятен, остаётся всего лишь составить таблицы сложения для упрощения процесса вычисления. Аналогично таблице умножения арабскими цифрами.

Сложение:

Сложение для старших разрядов:

Вычитание:

167 – 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000): CLXVII — XIIII = CL + X — X + VII — IIII = CLIII = 153

Вычитание римскими цифрами проще сложения. Знай себе вычитай из соответствующего разряда соответствующий разряд.

Таблица умножения:

Таблица умножения старших цифр:

Выпускники 11 класса, предложили преобразование типа:

a + b = b + a
ab = ba
a(b + c) = ab + ac

XXXX = X х (IIII)
В переводе на арабские цифры:
40 = 10 х 4
Пример вычисления:
167 х 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000):
CLXVII х XIIII = CLXVII х X + CLXVII х IIII = MMCCCXXXVIII
Подробности:
CLXVII х X = MDCLXX
CLXVII х IIII = CCCC + CC + XXXX + XX + VIII = DCLXVIII
MDCLXX + DCLXVIII = MMCCCXXXVIII = 2338

Сложности с вычислениями отсутствуют, только запись результата длинная, нужно привыкнуть к этому. Но сами вычисления легки и понятны.

Деление использует тот же алгоритм, что и деление уголком при помощи арабских цифр. И в то же время идентично делению многочлена на одночлен.

167 / 14 соответствует (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000):
CLXVII / XIIII = (CLX + VII) / (X + IIII) = CLX / (X + IIII) + VII / (X + IIII)
CLX / (X + IIII) = XVI х X / XIIII = (XVI / XIIII) х X = X + XX/ XIII =
= XI + VI / XIIII
X I + VI / XIIII + VII / (X + IIII) = XI + XIII / XIIII = 11 целых и 13/ 14 в остатке.

Возведение в степень и извлечение корней.

Возведение в любую степень легко выполняется по правилам умножения.
И возведения в степень по правилам нахождения степени суммы слагаемых.
Удобно использовать заранее составленные таблицы степеней.
Например, 14 в квадрате: XIIII х XIIII = X х X + II х X х IIII + IIII х IIII =
= C + LXXX + XVI = CLXXXXVI = 196

Извлечение корней можно проводить по известным алгоритмам.

На основании вышеизложенного следует вывод:
Арифметические вычисления римскими цифрами возможны и легко осуществимы, при соответствующем навыке.

Вычисления римскими цифрами более просты, образны и наглядны чем вычисления арабскими цифрами. Опытным путём установлено, что обучаемые усваивают арифметические операции со скоростью на порядки быстрее, чем арабскими цифрами и с минимальными усилиями. Перспективно создание учебника арифметики на базе римских цифр для классов, начиная с первого. В проекте участвовали ученики 11 класса.

Из Википедии: «Римские цифры – это цифры, использовавшиеся древними римлянами в их непозиционной системе счисления. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая стоит перед большей, то меньшая вычитается из большей (принцип вычитания).

Римские обозначения чисел известны лучше, чем любая другая древняя система счисления. Объясняется это огромным влиянием, которым пользовалась римская империя в прошлом. В целом римляне избегали заниматься математикой, поэтому у них отсутствовала потребность в больших числах. Однако, для обозначения 10000 они эпизодически использовали символ CCIƆƆ, а для числа 100000 – символ CCCIƆƆƆ. Дробей римляне избегали так же упорно, как и больших чисел.

Зададимся вопросом, как могло получиться, что империя в которой избегали заниматься математикой, смогла образоваться? Как учёные смогли научить других? Представьте ученика выпускного класса, у которого отсутствуют знания по сложению больших чисел, понятие о дробях и аллергия на математику. Чему, у него сможет научиться, например, первоклассник? Вероятно, мату, драться, прогуливать уроки и ещё чему-нибудь в том же духе.

Изложение исследования Игоря Шкурина о происхождении римских цифр.
Сейчас в источниках по истории математики можно прочитать, что отсутствуют достоверные сведения о происхождении римских цифр.

В 2011 году Игорю удалось реконструировать древний пальцевый счёт, основанный на десятичной позиционной системе и установить, что начертание римских цифр является упрощённым, пиктографическим изображением пальцев рук при таком счёте.

Кроме того, выявлено происхождение от упомянутого пальцевого счета важнейших механических счётных приспособлений древности: римских и греческих счётных досок абак, средневековых счётных «шахматных досок», японских счёты – «soroban», китайских – «suanpan» и прочих.

Первоначальное написание цифры 4, отличалось от сегодняшнего IV (то есть = 5 — 1), а раньше было IIII. Первоначальное написание цифры 9 было IX (то есть = 10 — 1), поэтому её будем писать, как VIIII.

Например, в древнеримском календаре «parapegma», при написании чисел 4, 9, 14, 19, 24 и 29 используется четырёхкратное повторение символов IIII.

На медали 1821 года четырёхкратное повторение символов: XXXX и IIII

Первоначальный правильный вид римских цифр такой:
1 — I
2 — II
3 — III
4 — IIII
5 — V
6 — VI
7 — VII
8 — VIII
9 — VIIII

Теперь эти римские цифры можно легко показать на пальцах одной правой руки, считая большой палец = 5, а остальные = 1, то есть цифре V соответствует отставленный большой палец. Сжатая в кулак рука по форме и значению соответствует цифре «ноль» (фактически ноль был, но при написании — отсутствовал). Как видно, написание всех римских цифр является упрощённым изображением фигур, образуемых при счёте на пальцах рук.

На левой руке показываются десятки, поэтому большой палец левой руки имеет значение 50 (римский символ L – сокращение от латинского laeva homo – левая рука), а остальные – по 10 (римский символ X, состоящий из двух V, т.е. = 5 + 5). Итак, римские цифры до 10 – это легко узнаваемые пиктограммы древнего пальцевого счёта.

Главным минусом римских цифр обычно называют отсутствие позиционной записи, которая, будто бы, затрудняет вычисления на бумаге. Во-первых, считали на пальцах или счётной доске «абак» с большой скоростью и потом лишь записывали результаты, а во-вторых, восприятие цифр зависит исключительно от привычки, которая при потребности возникает очень быстро, поскольку принцип очень простой: «одна рука – одно число». Например, показанное на двух руках число 10 выглядит легко узнаваемым – слева 1, а справа 0.

Такая десятичная позиционная система счёта позволяет на двух руках считать до 99. А если слева от вас встанет еще один человек, то вы вдвоём легко сможете делать сложение и вычитание на пальцах уже до 9999!
При этом пальцы правой руки второго человека имеют такое значение: большой палец – 500 и обозначается символом «D» от латинского Dextro homo – правая рука, а остальные – по 100 и обозначаются символом «C» от латинского Centum – сто.

Четыре пальца левой руки второго человека имеют значение 1000 и символ «M» от латинского Mille – тысяча, а вот для большого пальца левой руки второго человека, который имеет значение 5000, а также и для пальцев рук третьего человека и так далее, общераспространённые символы отсутствуют.

Например, два человека могут показать на пальцах число 2012, которое в римской записи выглядит как MMXII.

От счёта на пальцах ведёт своё происхождение, основанная на тех же самых принципах, древняя счётная доска абак, на которой «пальцы рук» обозначались камешками или косточками, что было гораздо удобнее для больших вычислений, свои руки свободны и можно обойтись без дополнительных людей.

Схема древнего пальцевого счета на римской счётной доске абак реализована следующим образом:

1. каждой руке соответствует свой вертикальный желобок, на котором расположены пять «пальцев» – камешков (косточек, шариков);
2. верхний камешек (обычно чёрного цвета) соответствует большому пальцу руки. В зависимости от того, в каком желобке он находится, имеет значение равное 5, 50, 500, 5000 и так далее (справа налево)
3. нижние 4 камешка (обычно более светлые) соответствуют остальным пальцам руки. В зависимости от того, в каком желобке находятся, имеют значение равное 1, 10, 100, 1000 и так далее (справа налево);
4. чтобы показать число на руке, разгибали нужные пальцы, а на счётной доске передвигали соответствующие камешки к середине, в счётное поле (на фото – в среднюю часть желобков).

Показанный на фото абак, выполнен из камня по схеме пальцевого счета. В четырёх желобках слева, камешки находятся в крайних положениях (пальцы этих рук загнуты), в средней счётной части отсутствуют камешки, то есть в этих разрядах – 0000. Далее в средней счётной части желобков набрано число 1992516. При помощи данного абака, можно считать до 10 миллиардов!

На следующей фотографии – реконструкция древнеримского абака, выполненная в 1977 году для музея в городе Майнц. Его бронзовый оригинал находится во французской Национальной библиотеке в Париже. Часть шариков – отсутствует, но смысл – понятен.

В данной конструкции абака есть отличия: справа сделаны дополнительные линии для дробей, есть обозначения разрядов, вместо перекатывания шариков в среднюю область счёта, применяется более удобный способ передвижение их к средней линии для счёта.

Древнеримские счёты абак сохранились у японцев под названием – soroban. Они используются для обучения в школах почти во всей Юго-Восточной Азии. Освоение счёта на соробане рекомендуется детям с 5 лет, поэтому, школьники легко складывают на соробане три шестизначных числа за 2 секунды.

Структура японских счетов соробан повторяет счётную доску абак, только косточки передвигаются по проволоке, вместо желобов. Счётным полем в соробане, как и на бронзовом абаке, служит счётная линия, к которой передвигаются косточки. Косточки в японском соробане соответствуют пальцам в древнем пальцевом счёте.

Одиночные верхние косточки имеют значение (справа налево): 5, 50, 500 и т.д., а расположенные по четыре нижние косточки соответственно по 1, 10, 100 и т.д. Числа набираются путём передвижения костяшек к счётной линии посередине, числа получаются интуитивно-понятными, поскольку старшие разряды расположены слева, а младшие – справа.

В Китае используется другая разновидность абака – суаньпан.

Этимология слов digital calculator, которые переводятся как «цифровой калькулятор» или «цифровой вычислитель», восходит к первоначальному значению «пальцевый камешковый». Английское слово digit переводится как «цифра», но на латинском языке digit – палец. Для примера растение наперстянка (от старославянского перст – палец, сейчас на болгарском палец — пръст [прыст]) на латинском – digitalis. Слово калькулятор (calculator) происходит от латинского слова calculus — маленький камешек, используемый для подсчёта. Поэтому настоящий digital calculator – это счётная доска с камешками, основанная на принципе пальцевого счета.

Можно самому сделать древнейший калькулятор. Нужно провести вертикальные линии – колонки на бумаге, песке, земле и использовать любой счётный материал – камешки, косточки, шашки, монеты, описанным выше способом. Именно так поступали во всём мире до 19 века. Расчертив сукно и столы («счёт на линиях») и используя при этом специальные счётные жетоны или деньги. Например, Казначейство Великобритании, именно поэтому, называлось «Палата Шахматной Доски».

Интересный момент – римские цифры возникли как упрощённое изображение разогнутых пальцев при пальцевом счёте, и до сих пор в Европе при счёте пальцы разгибают, а России наоборот – загибают. Возможно, от этого пошло выражение «загибаешь», в смысле «преувеличиваешь». В России каждый палец обозначал единицу (до десяти считали на двух руках), то для адаптации к сложившейся практике русские счёты были сделаны в виде удвоенного абака, где все косточки имеют значение единицы.

Возможно, именно из-за всемирного широчайшего распространения счётных приспособлений, основанных на десятичной позиционной системе древнего пальцевого счета, и были вытеснены из практики гораздо более удобные для умножения и деления двенадцатеричная и шестнадцатеричная системы счисления.

Уточнение к статье. Многие исследователи доказали, что все «древние римские» изобретения датируются 19 веком. Возможно, более удобные системы счисления, были специально заменены на менее удобные, с целью замедлить развития человека или запутать историю.